题目内容
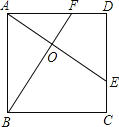
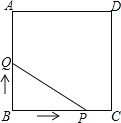
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.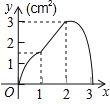 B.
B.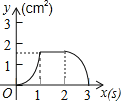
C.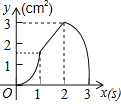 D.
D.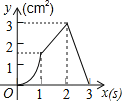
【答案】C
【解析】
试题分析:首先根据正方形的边长与动点P、Q的速度可知动点Q始终在AB边上,而动点P可以在BC边、CD边、AD边上,再分三种情况进行讨论:①0≤x≤1;②1<x≤2;③2<x≤3;分别求出y关于x的函数解析式,然后根据函数的图象与性质即可求解.
解:由题意可得BQ=x.
①0≤x≤1时,P点在BC边上,BP=3x,
则△BPQ的面积=![]() BPBQ,
BPBQ,
解y=![]() 3xx=
3xx=![]() x2;故A选项错误;
x2;故A选项错误;
②1<x≤2时,P点在CD边上,
则△BPQ的面积=![]() BQBC,
BQBC,
解y=![]() x3=
x3=![]() x;故B选项错误;
x;故B选项错误;
③2<x≤3时,P点在AD边上,AP=9﹣3x,
则△BPQ的面积=![]() APBQ,
APBQ,
解y=![]() (9﹣3x)x=
(9﹣3x)x=![]() x﹣
x﹣![]() x2;故D选项错误.
x2;故D选项错误.
故选:C.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目