题目内容
如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次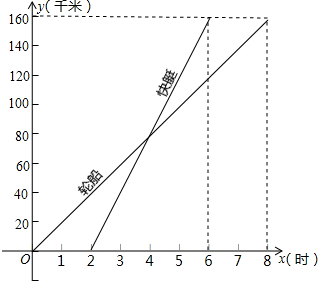 函数图象).根据图象解答下列问题:
函数图象).根据图象解答下列问题:(1)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)问快艇出发多长时间赶上轮船?
分析:(1)可根据图中给出的信息,用待定系数法分别求出轮船与快艇的函数关系式.
(2)可根据轮船与快艇到乙港时用的时间和走的路程,根据速度=路程÷时间,求出速度是多少.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
(2)可根据轮船与快艇到乙港时用的时间和走的路程,根据速度=路程÷时间,求出速度是多少.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
解答:解:(1)设表示轮船行驶过程的函数式为y=kx.由图象知:
当x=8时,y=160.
∴8k=160,解得:k=20
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴
,
解得
因此表示快艇行驶过程的函数解析式为y=40x-80;
(2)由图象可知,轮船在8小时内行驶了160千米.快艇在4小时内行驶了160千米.
故轮船在途中的行驶速度为160÷8=20(千米/时)
快艇在途中行驶的速度为160÷6=
(千米/时);
(3)设轮船出发x小时后快艇追上轮船.
20x=40x-80,
x=4,
则x-2=2.
答:快艇出发2小时后赶上轮船.
当x=8时,y=160.
∴8k=160,解得:k=20
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴
|
解得
|
因此表示快艇行驶过程的函数解析式为y=40x-80;
(2)由图象可知,轮船在8小时内行驶了160千米.快艇在4小时内行驶了160千米.
故轮船在途中的行驶速度为160÷8=20(千米/时)
快艇在途中行驶的速度为160÷6=
| 80 |
| 3 |
(3)设轮船出发x小时后快艇追上轮船.
20x=40x-80,
x=4,
则x-2=2.
答:快艇出发2小时后赶上轮船.
点评:本题是利用一次函数的有关知识解答实际应用题,本题中读懂图象是解题的关键.

练习册系列答案
相关题目
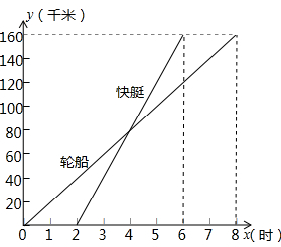 到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题: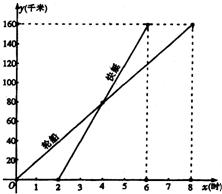 22、如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象.根据图象解答下列问题:
22、如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象.根据图象解答下列问题: 15、如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港行驶过程中路程随时间变化的图象,从图中可以看出,快艇出发
15、如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港行驶过程中路程随时间变化的图象,从图中可以看出,快艇出发 26、如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象.根据图象解答下列问题:
26、如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象.根据图象解答下列问题: