题目内容
已知A、B两个海港相距180海里.如图表示一艘轮船和一艘快艇沿相同路线从A港出发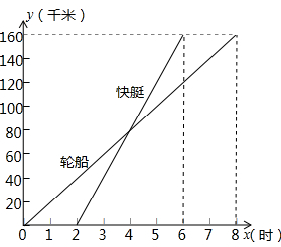 到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:(1)请分别求出表示轮船和快艇行驶过程的函数表达式(不要求写出自变量的取值范围);
(2)快艇出发多长时间后能超过轮船?
(3)快艇和轮船哪一艘先到达B港?
分析:根据图象获取相关信息:行使160海里轮船用时8小时,快艇用时4小时;快艇比轮船晚2小时出发.
(1)根据图象过特殊点,用待定系数法分别求关系式;
(2)通过解方程组求两函数的交点坐标后回答问题;
(3)通过图象可知快艇先到达B港.
(1)根据图象过特殊点,用待定系数法分别求关系式;
(2)通过解方程组求两函数的交点坐标后回答问题;
(3)通过图象可知快艇先到达B港.
解答:解:(1)∵轮船的函数图象经过点(0,0)、(8,160),
∴y轮船=20x;
同理,快艇的函数图象经过点(2,0)、(6,160),
∴
,解得
.
∴y快艇=40x-80.
(2)令y轮船=y快艇,得到20x=40x-80,
解得 x=4.
所以快艇出发(4-2)=2小时可超过轮船;
(3)观察图象可知快艇先到达B港.
∴y轮船=20x;
同理,快艇的函数图象经过点(2,0)、(6,160),
∴
|
|
∴y快艇=40x-80.
(2)令y轮船=y快艇,得到20x=40x-80,
解得 x=4.
所以快艇出发(4-2)=2小时可超过轮船;
(3)观察图象可知快艇先到达B港.
点评:此题考查一次函数及其图象的应用,通过观察图象获取相关信息是关键.

练习册系列答案
相关题目
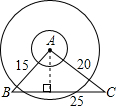
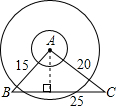 如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
如图所示,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.