题目内容
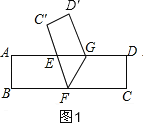
【题目】如图1,在一张矩形纸片ABCD上任意画一条线段GF,将纸片沿线段GF折叠,

(1)重叠部分的△EFG是等腰三角形吗?请说明理由.
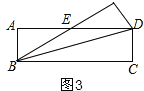
(2)若使点C与点A重合,折叠为GF,如图2,△AFG的面积记为S1,图3中沿BD折叠,△EBD的面积记为S2,试问S1和S2相等吗?请说明理由.
【答案】见解析
【解析】
试题分析:(1)如图1,证明∠EFG=∠AGF,则△EFG是等腰三角形;
(2)如图2,设AG=a,利用勾股定理表示出a,如图3,设ED=x,利用勾股定理表示出x,由a=x,所以AG=ED,所以S1和S2相等.
解:(1)如图1,△EFG是等腰三角形,理由是:
由折叠得:∠EFG=∠GFC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AGF=∠GFC,
∴∠EFG=∠AGF,
∴△EFG是等腰三角形,
(2)S1和S2相等,理由是:
如图2,∵△AFG是等腰三角形,
∴AF=AG,
设AG=a,则AF=FC=a,BF=BC﹣a,
在Rt△ABF中,由勾股定理得:AF2=AB2+BF2,
∴a2=(BC﹣a)2+AB2,
∴a=![]() ,
,
如图3,∵△BED是等腰三角形,
∴BE=ED,
设ED=x,则BE=x,AE=AD﹣x,
在Rt△ABE中,由勾股定理得:BE2=AB2+AE2,
x2=AB2+(AD﹣x)2,
x=![]() ,
,
∵AD=BC,
∴a=x,
即AG=ED,
∵S1=![]() AGAB,S2=
AGAB,S2=![]() EDAB,
EDAB,
∴S1=S2.


练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目