题目内容
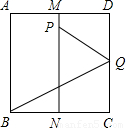
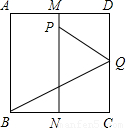
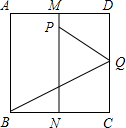 如图所示,有一块面积为1的正方形纸片ABCD,M、N分别为AD、BC的边上中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.
如图所示,有一块面积为1的正方形纸片ABCD,M、N分别为AD、BC的边上中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.(1)求MP;
(2)求证:以PQ为边长的正方形的面积等于
| 1 | 3 |
分析:(1)根据折叠的性质,可得BQ垂直平分PC;
进而可得△PBC是等边三角形,故可得PN的值.
根据图形的关系可MP=MN-PN,代入数据可得答案;
(2)根据折叠的性质,可得PQ=QC,∠PBQ=∠QBC=30°;
再在Rt△BCQ中,根据三角函数的定义可求得PQ的值,进而可得答案.
进而可得△PBC是等边三角形,故可得PN的值.
根据图形的关系可MP=MN-PN,代入数据可得答案;
(2)根据折叠的性质,可得PQ=QC,∠PBQ=∠QBC=30°;
再在Rt△BCQ中,根据三角函数的定义可求得PQ的值,进而可得答案.
解答: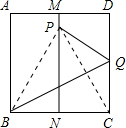 (1)解:连接BP、PC,由折法知点P是点C关于折痕BQ的对称点.
(1)解:连接BP、PC,由折法知点P是点C关于折痕BQ的对称点.
∴BQ垂直平分PC,BC=BP.
又∵M、N分别为AD、BC边上的中点,且ABCD是正方形,
∴BP=PC.
∴BC=BP=PC.
∴△PBC是等边三角形.
∵PN⊥BC于N,BN=NC=
BC=
,∠BPN=
×∠BPC=30°,
∴PN=
,MP=MN-PN=
.
(2)证明:由折法知PQ=QC,∠PBQ=∠QBC=30°.
在Rt△BCQ中,QC=BC•tan30°=1×
=
,
∴PQ=
.
∴以PQ为边的正方形的面积为
.
 (1)解:连接BP、PC,由折法知点P是点C关于折痕BQ的对称点.
(1)解:连接BP、PC,由折法知点P是点C关于折痕BQ的对称点.∴BQ垂直平分PC,BC=BP.
又∵M、N分别为AD、BC边上的中点,且ABCD是正方形,
∴BP=PC.
∴BC=BP=PC.
∴△PBC是等边三角形.
∵PN⊥BC于N,BN=NC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PN=
| ||
| 2 |
2-
| ||
| 2 |
(2)证明:由折法知PQ=QC,∠PBQ=∠QBC=30°.
在Rt△BCQ中,QC=BC•tan30°=1×
| ||
| 3 |
| ||
| 3 |
∴PQ=
| ||
| 3 |
∴以PQ为边的正方形的面积为
| 1 |
| 3 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 如图所示,有一块长32米,宽20米的矩形稻田ABCD,稻田内有两条处处等宽的弯曲小路,已知种植面积为540m2,求道路的宽是多少?
如图所示,有一块长32米,宽20米的矩形稻田ABCD,稻田内有两条处处等宽的弯曲小路,已知种植面积为540m2,求道路的宽是多少?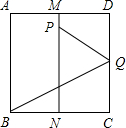 如图所示,有一块面积为1的正方形纸片ABCD,M、N分别为AD、BC的边上中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.
如图所示,有一块面积为1的正方形纸片ABCD,M、N分别为AD、BC的边上中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ. .
. .
.
 .
.