Question

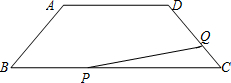如图，在等腰梯形ABCD中，AD=4，BC=9，∠B=45°．动点P从点B出发沿BC向点C运动，动点Q同时以相同速度从点C出发沿CD向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动．
（1）求AB的长；
（2）设BP=x，问当x为何值时△PCQ的面积最大，并求出最大值；
（3）探究：在AB边上是否存在点M，使得四边形PCQM为菱形？请说明理由．

Answer 1

分析：（1）作AE⊥BC，根据题意可知BE的长度，再根据∠B的正弦值，即可推出AB的长度；
（2）作QF⊥BC，根据题意推出BP=CQ，推出CP关于x的表达式，然后根据∠C的正弦值推出高QF关于x的表达式，即可推出面积关于x的二次函数式，最后根据二次函数的最值即可推出x的值；
（3）首先假设存在M点，然后根据菱形的性质推出，若存在，则PC=QC，9-x=x，x=

9

2

，得出矛盾，所以假设是错误的，故AB上不存在M点．

解答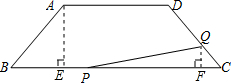：解：（1）作AE⊥BC，
∵等腰梯形ABCD中，AD=4，BC=9，
∴BE=（BC-AD）÷2=2.5，
∵∠B=45°，
∴AB=

5 2

2

；

（2）作QF⊥BC，
∵等腰梯形ABCD，
∴∠B=∠C=45°，则△CQF是等腰直角三角形．
∵点P和点Q的运动速度、运动时间相同，BP=x，
∴BP=CQ=x，
∵BC=9，
∴CP=9-x，QF=

2

2

x，
设△PQC的面积为y，
∴y=（9-x）•

2

2

x•

1

2

，
即y=-

2

4

x2+

9 2

4

x=-

2

4

(x-

9

2

)2+

81 2

16

，
∵AB=

5 2

2

，动点P从点B出发沿BC向点C运动，动点Q同时以相同速度从点C出发沿CD向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动．BP=x，
∴0＜x≤

5 2

2

＜

9

2

，
∴当x=

5 2

2

时，△PQC的面积最大，最大值为：
y=

1

2

PC•QF=

1

2

（9-

5

2

2

）×

5

2

=

45

4

-

25 2

8

；

（3）不存在，
若存在，则PC=QC，
∴9-x=x，
∴x=

9

2

，
而

9

2

＞

5

2

2

，
∴边AB上不存在点M，使得四边形PCQM为菱形．

点评：本题主要考查等腰梯形的性质、解直角三角形、二次函数的最值、内角和定理、菱形的性质，关键在于根据图形画出相应的辅助线，熟练掌握相关的性质定理即可．