题目内容
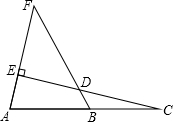如图，C在AB的延长线上，CE⊥AF于E，交FB于D，若∠F=40°，∠C=20°，则∠FBA=70°
70°
．分析：根据垂直定义和三角形的内角和定理求出∠EDF的度数，再根据三角形外角的性质，求出∠FBA的度数．
解答：解：∵CE⊥AF于E，
∴∠FED=90°，
又∵∠F=40°，
∴∠FDE=90°-40°=50°，
∴∠CDB=50°，
又∵∠C=2O°，
∴∠FBA=20°+50°=70°．
故答案为70°．
∴∠FED=90°，
又∵∠F=40°，
∴∠FDE=90°-40°=50°，
∴∠CDB=50°，
又∵∠C=2O°，
∴∠FBA=20°+50°=70°．
故答案为70°．
点评：本题考查了三角形内角和定理和三角形内角、外角的关系，难度不大，但很巧妙．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
如图点D在△ABC的AB边上，AD=BD=CD=1，延长BC至E，BC=CE，连接AE，则AE=
