题目内容
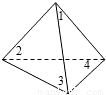
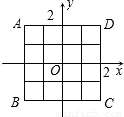
如图，放在直角坐标系中的正方形ABCD的边长为4．现做如下实验：转盘被划分成4个相同的小扇形，并分别标上数字1，2，3，4，分别转动两次转盘，转盘停止后，指针所指向的数字作为直角坐标系中M点的坐标（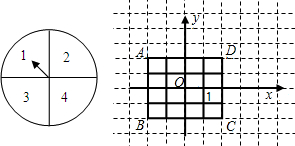
第一次作横坐标，第二次作纵坐标），指针如果指向分界线上，则重新转动转盘．（1）请你用树状图或列表的方法，求M点落在正方形ABCD面上（含内部与边界）的概率；
（2）将正方形ABCD平移整数个单位，则是否存在某种平移，使点M落在正方形ABCD面上的概率为
| 3 | 4 |
分析：（1）用列表法，把点M的坐标的16种情况都表示出来，可知中落在正方形ABCD面上（含内部与边界）的有（1，1），（1，2），（2，1），（2，2），共4种，所以M点落在正方形ABCD面上（含内部与边界）的概率是
=
；
（2）若使点M落在正方形ABCD面上的概率为
，则只有4个点不在正方形内部．并且点M的所有情况都是在第1象限，所以可以通过向右平移2个单位长度，再向上平移1个单位长度或者向右平移1个单位长度，向上平移2个单位长度使点M落在正方形ABCD面上的概率为
．
| 4 |
| 16 |
| 1 |
| 4 |
（2）若使点M落在正方形ABCD面上的概率为
| 3 |
| 4 |
| 3 |
| 4 |
解答：解：（1）正方形四个顶点的坐标分别是A（-2，2）；B（-2，-2）；C（2，-2）；D（2，2），
列表得：
M点的坐标所有的情况有共16种，
其中落在正方形ABCD面上（含内部与边界）的有（1，1），（1，2），（2，1），（2，2），共4种，所以M点落在正方形ABCD面上（含内部与边界）的概率是
=
；
（2）若使点M落在正方形ABCD面上的概率为
，则只有4个点不在正方形内部，所以可把正方形ABCD向右平移2个单位长度，再向上平移1个单位长度或者向右平移1个单位长度，向上平移2个单位长度即可．
列表得：
| a b |
1 | 2 | 3 | 4 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
其中落在正方形ABCD面上（含内部与边界）的有（1，1），（1，2），（2，1），（2，2），共4种，所以M点落在正方形ABCD面上（含内部与边界）的概率是
| 4 |
| 16 |
| 1 |
| 4 |
（2）若使点M落在正方形ABCD面上的概率为
| 3 |
| 4 |
点评：主要考查了概率的求算方法和正方形与平移的有关性质．要会根据正方形的性质得到所对应的点的坐标，利用列表法求算符合条件的概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
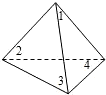
（一）如图，放在直角坐标系中的正方形ABCD的边长为4．现做如下实验：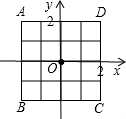
如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．
？若存在，指出其中的一种平移方式；若不存在，请说明理由；
