题目内容
若实数范围内定义一种运算“※”，其规则为a※b=| 1 |
| a |
| 1 |
| b |
分析：根据a※b=
-
，推出x※（2x+1）的展开形式，然后解方程即可．
| 1 |
| a |
| 1 |
| b |
解答：解：∵a※b=
-
，
∴x※（2x+1）=
-
=
=
，
又∵x※（2x+1）=0，
∴
=0，
解得：x=-1，
经检验得x=-1是方程的根．
故答案为：-1．
| 1 |
| a |
| 1 |
| b |
∴x※（2x+1）=
| 1 |
| x |
| 1 |
| 2x+1 |
| 2x+1-x |
| x(2x+1) |
| x+1 |
| 2x2+x |
又∵x※（2x+1）=0，
∴
| x+1 |
| 2x2+x |
解得：x=-1，
经检验得x=-1是方程的根．
故答案为：-1．
点评：此题主要考查了实数的运算，也考查了解分式方程，属于新定义题型，首先要分析好定义式的形式，关键是弄清a、b各代表所给式子中哪一个代数式，然后再根据所的规律进行解题．
练习册系列答案
阅读快车系列答案
相关题目
若实数范围内定义一种运算“﹡”，使a*b=（a+1）2-ab，则方程（x+2）*5=0的解为（ ）
| A、-2 | ||||||||
| B、-2，3 | ||||||||
C、
| ||||||||
D、
|
－
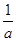，根据这个规则，若x※(2x+1)=0，则x=____________
-
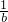，根据这个规则，若x※（2x+1）=0，则x=________．