题目内容
【题目】如图，AB是⊙O的直径，C、D是圆上的两点．若BC=8，cosD=
， 则AB的长为（ ）
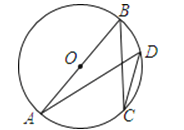
A.
B.
C.
D.12
【答案】D
【解析】解：连接AC，
由圆周角定理得，∠B=∠D，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴cosB=
， 又BC=8，
∴AB=12，
故选：D．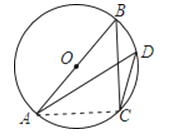
【考点精析】关于本题考查的圆周角定理和解直角三角形，需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．
练习册系列答案
相关题目
