题目内容
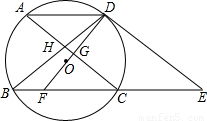
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及其延长线分别交AC、BC于点G、F.
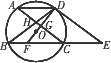
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5 cm,AC=8 cm,求⊙O的半径.
答案:
解析:
解析:
|
(1)证明:因为DE是⊙O的切线,且DF过圆心O, 所以DF⊥DE. 又因为AC∥DE, 所以DF⊥AC. 所以DF垂直平分AC. (2)证明:由(1)知:AG=GC. 又因为AD∥BC, 所以∠DAG=∠FCG. 又因为∠AGD=∠CGF, 所以△AGD≌△CGF(ASA). 所以AD=FC. 因为AD∥BC且AC∥DE, 所以四边形ACED是平行四边形. 所以AD=CE. 所以FC=CE. (3)解:连接AO, 因为AG=GC,AC=8 cm, 所以AG=4 cm. 在Rt△AGD中,由勾股定理得GD= 设圆的半径为r,则AO=r,OG=r-3, 在Rt△AOG中,由勾股定理得AO2=OG2+AG2, 即r2=(r-3)2+42,解得r= 所以⊙O的半径为 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
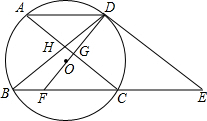 延长线分别交AC、BC于点G、F.
延长线分别交AC、BC于点G、F.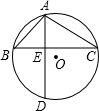 已知:如图,⊙O的弦AD、BC互相垂直,垂足为E,∠BAD=∠α,∠CAD=∠β,且siaα=
已知:如图,⊙O的弦AD、BC互相垂直,垂足为E,∠BAD=∠α,∠CAD=∠β,且siaα=
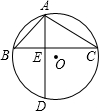 已知:如图,⊙O的弦AD、BC互相垂直,垂足为E,∠BAD=∠α,∠CAD=∠β,且siaα=
已知:如图,⊙O的弦AD、BC互相垂直,垂足为E,∠BAD=∠α,∠CAD=∠β,且siaα= ,cosβ=
,cosβ= ,AC=2.
,AC=2.