题目内容
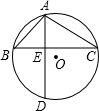已知：如图，⊙O的弦AD、BC互相垂直，垂足为E，∠BAD=∠α，∠CAD=∠β，且siaα=| 3 |
| 5 |
| 1 |
| 3 |
求（1）EC的长；
（2）AD的长．
分析：要求EC的长，在直角三角形ACE中，首先根据cosβ=
，AC=2，求得AE的长，再根据勾股定理求得EC的长；要求AD的长，根据相交弦定理只需求得BE的长，根据sinα=
，求得cosα=
，从而求得AB的长，再根据勾股定理求得BE的长即可．
| 1 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
解答：解：（1）在直角三角形ACE中，AE=AC•cosβ=
再根据勾股定理，得EC=
=
；
（2）在直角三角形ABE中，
根据sinα=
，求得cosα=
，则AB=
=
再根据勾股定理，得BE=
=
根据相交弦定理，得DE=
=
则AD=
+
．
| 2 |
| 3 |
再根据勾股定理，得EC=
4-
|
4
| ||
| 3 |
（2）在直角三角形ABE中，
根据sinα=
| 3 |
| 5 |
| 4 |
| 5 |
| AE |
| cosα |
| 5 |
| 6 |
再根据勾股定理，得BE=
|
| 1 |
| 2 |
根据相交弦定理，得DE=
| BE•CE |
| AE |
| 2 |
则AD=
| 2 |
| 2 |
| 3 |
点评：能够熟练运用锐角三角函数的概念、勾股定理以及相交弦定理进行求解．
练习册系列答案
高中必刷题系列答案
相关题目
16、已知：如图，⊙O的弦BE平分弦CD于点F，过点B的切线交DC的延长线于点A，且AC=BF=4，FE=9．求CF和AB的长．
16、已知：如图，⊙O的弦AB平分弦CD，AB=10，CD=8．且PA＜PB，则PB-PA=
（1997•四川）已知：如图，⊙O的弦AB、CD相交于点P，C是弧AB的中点，弦CE∥BD，交AB于点F．求证：AE•FP=AF•CP．
为
的弦，
于
，交
，
于
.
为
时，求阴影部分的面积.