题目内容
 如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.
如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.
(1)求月牙形公园的面积;
(2)现要在公园内建一块顶点都在⊙P上的直角三角形场地ABC,其中∠C=90°,求场地的最大面积.
解:(1)连接DQ、EQ、PD、PE、PQ、DE.

由已知PD=PQ=DQ,
∴△DPQ是等边三角形.
∴∠DQP=60°.
同理∠EQP=60°.
∴∠DQE=120°,
∵⊙P和⊙Q交于D、E,
∴QP⊥DE,DF=EF,
∵△DPQ是等边三角形,
∴∠QDE=30°,
∴FQ= DQ=1,
DQ=1,
由勾股定理得:DF= =EF,
=EF,
即ED=2 ,
,
S弓形DPE=S扇形QDE-S△DQE
=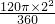 -
- ×2
×2 ×1
×1
=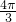 -
- ,
,
故月牙形公园的面积=4π-2( π-
π- )=(
)=( π﹢2
π﹢2 )km2.
)km2.
答:月牙形公园的面积为( π﹢2
π﹢2 )km2.
)km2.
(2)∵∠C=90°,
∴AB是⊙P的直径,
过点C作CN⊥AB于点N,S△ABC= CN•AB,
CN•AB,
∵AB=4km,
∴S△ABC的面积取最大值就是CN长度取最大值,即CN=CP=2km,
S△ABC的面积最大值等于4km2,
故场地的最大面积为4km2.
分析:(1)连接DQ、EQ、PD、PE、PQ、DE,得出等边三角形DPQ和等边三角形DPQ,得出∠PQD=∠EQP=60°,根据相交两圆的性质得出DE⊥PQ,求出FQ和DF的值,求出DE,分别求出扇形DQE的面积和三角形DEQ的面积,即可求出弓形DPE的面积,根据圆的面积和弓形的面积求出答案即可;
(2)根据∠ACB=90°得出AB是圆的直径,是2km,要使三角形ABC的面积最大得出只要高CN最大即可,得出CN的最大值是CP(P和N重合,CN最大),代入求出即可.
点评:本题考查了等边三角形的性质和判定,圆周角定理,勾股定理,含30度角的直角三角形性质,扇形的面积,三角形的面积,相交两圆的性质等知识点的综合运用,主要考查学生运用定理进行推理和计算的能力.

由已知PD=PQ=DQ,
∴△DPQ是等边三角形.
∴∠DQP=60°.
同理∠EQP=60°.
∴∠DQE=120°,
∵⊙P和⊙Q交于D、E,
∴QP⊥DE,DF=EF,
∵△DPQ是等边三角形,
∴∠QDE=30°,
∴FQ=
 DQ=1,
DQ=1,由勾股定理得:DF=
 =EF,
=EF,即ED=2
 ,
,S弓形DPE=S扇形QDE-S△DQE
=
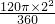 -
- ×2
×2 ×1
×1=
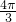 -
- ,
,故月牙形公园的面积=4π-2(
 π-
π- )=(
)=( π﹢2
π﹢2 )km2.
)km2.答:月牙形公园的面积为(
 π﹢2
π﹢2 )km2.
)km2.(2)∵∠C=90°,
∴AB是⊙P的直径,
过点C作CN⊥AB于点N,S△ABC=
 CN•AB,
CN•AB,∵AB=4km,
∴S△ABC的面积取最大值就是CN长度取最大值,即CN=CP=2km,
S△ABC的面积最大值等于4km2,
故场地的最大面积为4km2.
分析:(1)连接DQ、EQ、PD、PE、PQ、DE,得出等边三角形DPQ和等边三角形DPQ,得出∠PQD=∠EQP=60°,根据相交两圆的性质得出DE⊥PQ,求出FQ和DF的值,求出DE,分别求出扇形DQE的面积和三角形DEQ的面积,即可求出弓形DPE的面积,根据圆的面积和弓形的面积求出答案即可;
(2)根据∠ACB=90°得出AB是圆的直径,是2km,要使三角形ABC的面积最大得出只要高CN最大即可,得出CN的最大值是CP(P和N重合,CN最大),代入求出即可.
点评:本题考查了等边三角形的性质和判定,圆周角定理,勾股定理,含30度角的直角三角形性质,扇形的面积,三角形的面积,相交两圆的性质等知识点的综合运用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.
(2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.