题目内容
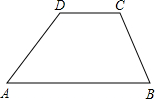 一个大坝的横截面是如图所示的梯形,其中AB∥CD,∠A=45°,∠B=60°,AD=8米,AB=15米.若坝长2千米,问这条坝共有多少土方(保留两个有效数字)?
一个大坝的横截面是如图所示的梯形,其中AB∥CD,∠A=45°,∠B=60°,AD=8米,AB=15米.若坝长2千米,问这条坝共有多少土方(保留两个有效数字)?
分析:作DE⊥AB、CF⊥AB,解Rt△ADE可以求得AE、DE的长,解Rt△BCF可以求得BF的长,进而求得CD的长,即可求得梯形的面积,根据坝长即可计算土方数.
解答: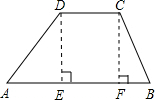 解:过D、C分别作DE⊥AB、CF⊥AB,
解:过D、C分别作DE⊥AB、CF⊥AB,
在Rt△ADE中,∠A=45°,AE=DE=AD•sinA=4
米,
在Rt△BCF中,∠B=60°,BF=CF•tan∠BCF=
米,
∴EF=AB-AE-BF=(15-4
-
)米,
∴梯形ABCD的面积=
(15+15-4
-
)×4
平方米
这条坝共有
(15+15-4
-
)×4
×2000个土方≈1.2×105立方米.
 解:过D、C分别作DE⊥AB、CF⊥AB,
解:过D、C分别作DE⊥AB、CF⊥AB,在Rt△ADE中,∠A=45°,AE=DE=AD•sinA=4
| 2 |
在Rt△BCF中,∠B=60°,BF=CF•tan∠BCF=
4
| ||
| 3 |
∴EF=AB-AE-BF=(15-4
| 2 |
4
| ||
| 3 |
∴梯形ABCD的面积=
| 1 |
| 2 |
| 2 |
4
| ||
| 3 |
| 2 |
这条坝共有
| 1 |
| 2 |
| 2 |
4
| ||
| 3 |
| 2 |
点评:本题考查了梯形面积的计算,三角函数值在直角三角形中的运用,本题中求梯形的面积是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 11、如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=
11、如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=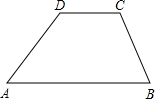 一个大坝的横截面是如图所示的梯形,其中AB∥CD,∠A=45°,∠B=60°,AD=8米,AB=15米.若坝长2千米,问这条坝共有多少土方(保留两个有效数字)?
一个大坝的横截面是如图所示的梯形,其中AB∥CD,∠A=45°,∠B=60°,AD=8米,AB=15米.若坝长2千米,问这条坝共有多少土方(保留两个有效数字)?