题目内容
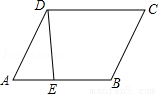
如图,已知E是平行四边形ABCD的边AB上的点,连接DE.
(1)在∠ABC的内部,作射线BM交线段CD于点F,使∠CBF=∠ADE;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)的条件下,求证:△ADE≌△CBF.
【答案】
(1)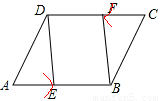 (2)证明见解析
(2)证明见解析
【解析】(1)解:作图如下:

(2)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC。
∵∠ADE=∠CBF,∴△ADE≌△CBF(ASA)。
(1)以点C为圆心,AC长为半径画弧,交CD于点F,连接BF,则∠CBF=∠ADE。
(2)根据平行四边形的性质可得∠A=∠C,AD=BC,由ASA可证△ADE≌△CBF

练习册系列答案
相关题目
 19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论: 如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点. 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是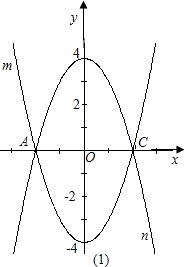

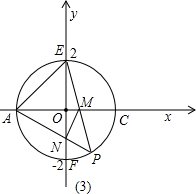
 如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为
如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为