题目内容
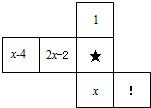8、如图是一个立方体的表面展开图，已知立方体相对两个面上的数值相同，则“★”、“！”面上的数分别为（ ）分析：根据立方体相对两个面上的数值相同，可知x=1，分别代入x-4，2x-2即可求出“★”、“！”面上的数．
解答：解：这是一个正方体的平面展开图，共有六个面，其中面“x”与面“1”相对，
面“★”与面“x-4”相对，
面“！”与面“2x-2”相对．
因为相对两个面上的数相同，
所以x=1，
∴★=x-4=-3，！=2x-2=0．
故选B．
面“★”与面“x-4”相对，
面“！”与面“2x-2”相对．
因为相对两个面上的数相同，
所以x=1，
∴★=x-4=-3，！=2x-2=0．
故选B．
点评：本题考查了正方体的空间图形，从相对面入手，分析及解答问题．解题的关键是由立方体相对两个面上的数值相同得到x的值．
练习册系列答案
相关题目
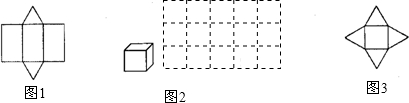
一个多面体的面数（a）和这个多面体表面展开后得到的平面图形的顶点数（b），棱数（c）之间存在一定规律，如图1是正三棱柱的表面展开图，它原有5个面，展开后有10个顶点（重合的顶点只算一个），14条棱．
【探索发现】
（1）请在图2中用实线画出立方体的一种表面展开图；
（2）请根据图2你所画的图和图3的四棱锥表面展开图填写下表：
| 多面体 | 面数a | 展开图的顶点数b | 展开图的棱数c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱锥 | ______ | 8 | 12 |
| 立方体 | ______ | ______ | ______ |
【解决问题】
（4）已知一个多面体表面展开图有17条棱，且展开图的顶点数比原多面体的面数多2，则这个多面体的面数是多少？