题目内容
关于x,y的方程x2+xy+2y2=29的整数解(x,y)的组数为( )A.2组
B.3组
C.4组
D.无穷多组
【答案】分析:首先将方程x2+xy+2y2=29看做是关于x的一元二次方程,根据判别式中△≥0,再根据x为整数根,且是完全平方数,确定出y2的取值.解得y值,进一步确定出x的值.
解答:解:可将原方程视为关于x的二次方程,将其变形为x2+yx+(2y2-29)=0.
由于该方程有整数根,则判别式△≥0,且是完全平方数.
由△=y2-4(2y2-29)=-7y2+116≥0,
解得y2≤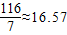 .于是
.于是
显然,只有y2=16时,△=4是完全平方数,符合要求.
当y=4时,原方程为x2+4x+3=0,此时x1=-1,x2=-3;
当y=-4时,原方程为x2-4x+3=0,此时x3=1,x4=3.
所以,原方程的整数解为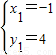
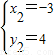
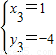
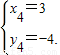
故选C.
点评:本题解题的关键是根据一次方程中根与系数的关系,利用判别式来求解.
解答:解:可将原方程视为关于x的二次方程,将其变形为x2+yx+(2y2-29)=0.
由于该方程有整数根,则判别式△≥0,且是完全平方数.
由△=y2-4(2y2-29)=-7y2+116≥0,
解得y2≤
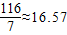 .于是
.于是 | y2 | 0 | 1 | 4 | 9 | 16 |
| △ | 116 | 109 | 88 | 53 | 4 |
当y=4时,原方程为x2+4x+3=0,此时x1=-1,x2=-3;
当y=-4时,原方程为x2-4x+3=0,此时x3=1,x4=3.
所以,原方程的整数解为
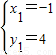
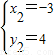
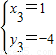
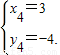
故选C.
点评:本题解题的关键是根据一次方程中根与系数的关系,利用判别式来求解.

练习册系列答案
相关题目
关于x,y的方程x2+xy+2y2=29的整数解(x,y)的组数为( )
| A、2组 | B、3组 | C、4组 | D、无穷多组 |