题目内容
【题目】已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F.
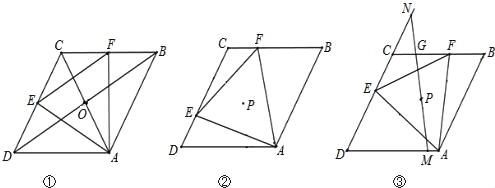
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
【答案】(1)略;(2)外心P一定落在直线DB上;2.
【解析】
试题(1)连接OE、OF,根据菱形得出AC⊥BD,BD平分∠ADC,AO=DC=BC,则∠COD=∠COB=∠AOD=90°,∠ADO=30°,根据E、F分别为中点得出OE=OF=OA,即外心;(2)分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,则∠PIE=∠PJD=90°,∠ADC=60°,∠IPJ=120°,根据点P是等边△AEF的外心得到∠EPA=120°,PE=PA,从而说明△PIE≌△PJA,即PI=PJ,从而得出结论;当AE⊥DC时.△AEF面积最小,此时点E、F分别为DC、CB中点,连接BD、AC交于点P,由(1)可得点P即为△AEF的外心,设DM=x,DN=y则CN=y-1,根据BC∥DA得到△GBP≌△MDP,则BG=DM=x,CG=1-x,根据BC∥DA得到△GBP∽△NDM则![]() ,即
,即![]() 从而得出结论.
从而得出结论.
试题解析:(1)证明:如图1,分别连接OE、0F,
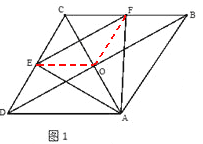
∵四边形ABCD是菱形,∴AC⊥BD,BD平分∠ADC.AO=DC=BC
∴∠COD=∠COB=∠AOD=90°, ∠ADO=![]() ∠ADC=
∠ADC=![]() ×60°=30°
×60°=30°
又∵E、F分别为DC、CB中点,∴OE=![]() CD,OF=
CD,OF=![]() BC,AO=
BC,AO=![]() AD
AD
∴0E=OF=OA ∴点O即为△AEF的外心。
(2)①猜想:外心P一定落在直线DB上。证明如下:
如图2,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,
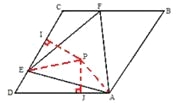
∴∠PIE=∠PJD=90° ∵∠ADC=60°,
∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120°,
∵点P是等边△AEF的外心, ∴∠EPA=120°,PE=PA ∴∠IPJ=∠EPA。
∴∠IPE=∠JPA,∴△PIE≌△PJA(AAS) ∴PI=PJ ∴点P在∠ADC的平分线上,即点P落在直线DB上
②![]() 为定值2
为定值2
当AE⊥DC时.△AEF面积最小,此时点E、F分别为DC、CB中点.
连接BD、AC交于点P,由(1)可得点P即为△AEF的外心 如图3.设MN交BC于点G,
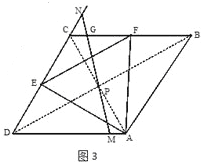
设DM=x,DN=y(x≠0.y≠O),则CN=y-1 ∵BC∥DA,∴△GBP≌△MDP
∴BG=DM=x. ∴CG=1-x ∵BC∥DA,∴△GBP∽△NDM
∴![]() ,即
,即![]() ∴x+y=2xy ∴
∴x+y=2xy ∴![]() ,即
,即![]() =2。
=2。

 口算题天天练系列答案
口算题天天练系列答案【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
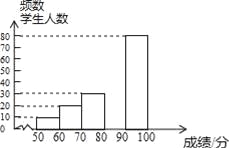
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?