题目内容
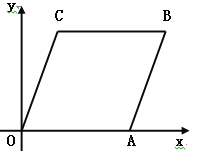
【题目】如图1,△ABC中,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B,C分别在AD,AF上,此时BD=CF,BD⊥CF成立.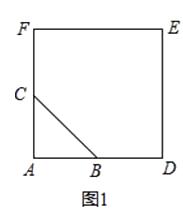
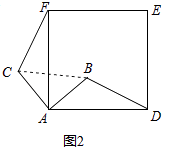
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交AF,CF于点N,H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段AN的长.
时,求线段AN的长.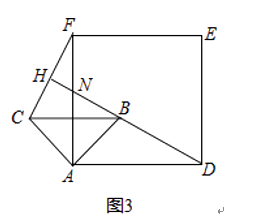
【答案】
(1)解:BD=CF.
理由如下:如图2中,由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,
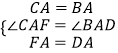 ,
,
∴△CAF≌△BAD,
∴BD=CF
(2)解:①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NDA=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF;
②如图3中,作BM⊥AD于M,
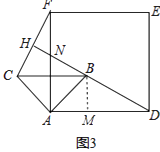
在Rt△AMB中,∵∠BAM=45°,AB=2,
∴AM=BM= ![]() ,DM=3
,DM=3 ![]() ﹣
﹣ ![]() =2
=2 ![]() ,
,
BM∥AN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AN= ![]()
【解析】(1)根据旋转变换的性质易证明△CAF≌△BAD,即可求证结论。
(2)①根据全等三角形的性质、△CAF≌△BAD,得出∠CFA=∠BDA,再证明∠FHN=90°,根据垂直的定义证明即可;
②作BM⊥AD于M,在Rt△AMB中,由∠BAM=45°,AB=2,推出AM=BM,求得DM、BM的长。再根据平行线分线段成比例得出比例式,建立方程即可求得AN的值。
【考点精析】通过灵活运用垂线的性质和平行线分线段成比例,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.

练习册系列答案
相关题目