题目内容
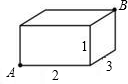
在一个长、宽、高分别为30cm，40cm，50cm的长方体盒子内，70cm长的木棒________放进．（填“能”或“不能”）
能
分析：在长方体的盒子中，一角的顶点与斜对的不共面的顶点的距离最大，根据木箱的长，宽，高可求出最大距离，然后和木棒的长度进行比较．
解答：因此可设放入长方体盒子中的最大长度是xcm，
根据题意，得x2=502+402+302=5000，
702=4900，
因为4900＜5000，所以能放进去．
故答案为能．
点评：考查了勾股定理的应用，本题的关键是求出木箱内木棒的最大长度．
分析：在长方体的盒子中，一角的顶点与斜对的不共面的顶点的距离最大，根据木箱的长，宽，高可求出最大距离，然后和木棒的长度进行比较．
解答：因此可设放入长方体盒子中的最大长度是xcm，
根据题意，得x2=502+402+302=5000，
702=4900，
因为4900＜5000，所以能放进去．
故答案为能．
点评：考查了勾股定理的应用，本题的关键是求出木箱内木棒的最大长度．
练习册系列答案
相关题目
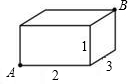如图，一个蚂蚁要在一个长，宽，高分别为2，3，1分米的长方体的表面从A点爬到B点，那么最短的路径是
如图，一个蚂蚁要在一个长，宽，高分别为2，3，1分米的长方体的表面从A点爬到B点，那么最短的路径是________分米．（结果可以保留根号）