Question

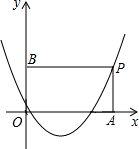
如图，P为抛物线y=x²-2x上对称轴右侧的一点，且点P在x轴上方，过点P作PA垂直x轴于点A，PB垂直y轴于点B，得到矩形PAOB．若PA=1．
（1）求点P的坐标；
（2）求矩形PAOB的面积．

Answer 1

分析：（1）根据PA=1可知，点P的纵坐标y=1，将其代入抛物线y=x²-2x即可求得点P的横坐标；
（2）根据点P的横纵坐标可知矩形PAOB的长与宽；由矩形的面积公式求得矩形PAOB的面积．

解答：解：（1）由题意得x²-2x=1…（2分）
解得x1=1+

2

x2=1-

2

（舍去）   …（4分）
∴点P的坐标为( 1+

2

 ， 1 )…（6分）

（2）S=1×(1+

2

)=1+

2

…（9分）
∴矩形PAOB的面积为1+

2

． …（10分）

点评：本题考查了二次函数图象上点的坐标特征、矩形的性质．根据题意求得点P的纵坐标是解题的关键．