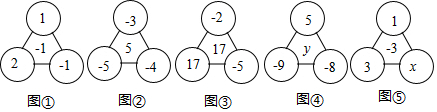
题目内容
13.关于函数y=2x2-3,y=-$\frac{1}{2}{x^2}$的图象及性质,下列说法不正确的是( )| A. | 它们的对称轴都是y轴 | |
| B. | 对于函数$y=-\frac{1}{2}{x^2}$,当x>0时,y随x的增大而减小 | |
| C. | 抛物线y=2x2-3不能由抛物线y=-$\frac{1}{2}{x^2}$平移得到 | |
| D. | 抛物线y=2x2-3的开口比y=-$\frac{1}{2}{x^2}$的开口宽 |
分析 由抛物线解析式可得出对称轴、增减性及开口大小等,再进行逐项判断即可.
解答 解:
在y=2x2-3中,对称轴为y轴,在y=-$\frac{1}{2}{x^2}$中对称轴为y轴,开口向下,当x>0时,y随x的增大而增大,
故A、B正确;
∵2≠-$\frac{1}{2}$,
∴抛物线y=2x2-3不能由抛物线y=-$\frac{1}{2}{x^2}$平移得到,故C正确;
∵2>|-$\frac{1}{2}$|,
∴抛物线y=2x2-3的开口比y=-$\frac{1}{2}{x^2}$的开口窄,故D不正确;
故选D.
点评 本题主要考查二次函数的性质,掌握二次函数的开口大小与二次项系数的大小有关是解题的关键.

练习册系列答案
相关题目
8.下列图形既是轴对称图形,又是中心对称图形的有( )个
①等边三角形 ②菱形 ③圆 ④正六边形 ⑤抛物线.
①等边三角形 ②菱形 ③圆 ④正六边形 ⑤抛物线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.现有四张分别标有数字1、2、2、3的卡片,他们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽出一张后放回,再背朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{11}{16}$ | D. | $\frac{1}{2}$ |