题目内容
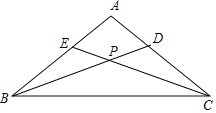
【题目】如图,在等腰△ABC中,AB=AC,CE、BD分别为∠ACB、∠ABC的角平分线,CE、BD相交于P.
(1)求证:CD=BE;
(2)若∠A=98°,求∠BPC的度数.
【答案】(1)详见解析;(2)139°
【解析】
(1)根据已知条件可由“ASA”证得△BCE≌△CBD,即可求得CD=BE;
(2)由三角形内角和定理以及CE、BD分别为∠ACB、∠ABC的角平分线可得∠BPC=180°-![]() ∠ABC+∠ACB,即可求解.
∠ABC+∠ACB,即可求解.
证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵CE、BD分别为∠ACB、∠ABC的角平分线
∴∠ABD=∠DBC=![]() ∠ABC,∠ACE=∠BCE=
∠ABC,∠ACE=∠BCE=![]() ∠ACB
∠ACB
∴∠DBC=∠BCE,且∠ABC=∠ACB,BC=BC
∴△BCE≌△CBD(ASA)
∴CD=BE,
(2)∵∠A=98°
∴∠ABC+∠ACB=82°
∴∠DBC+∠BCE=41°
∴∠BPC=180°﹣∠DBC﹣∠BCE=139°

练习册系列答案
相关题目