Question

【题目】如图1，已知抛物线经过点（9，10），交轴于点，直线∥轴，点是直线下方抛物线上的动点．

（1）直接写出抛物线的解析式为 ，点的坐标为 、的坐标为 _；

（2）过点且与轴平行的直线与直线、分别交于点、，当四边形的面积最大时，求点的坐标；

（3）如图2，当点为抛物线的顶点时，在直线上是否存在点，使得以、、为顶点的三角形与相似，若存在，求出点的坐标，若不存在，请说明理由．

Answer 1

【答案】（1），B（0,1），C（6,1）;（2）P（）；（3）Q（-3,1），或（4,1）.

【解析】分析：（1）由点A坐标可得抛物线解析式，求出x=0时y的值即可知点B坐标，再根据抛物线对称性得出点C坐标；

（2）设点P（m， m-2m+1），表示出PD=m+3m,再用S四边形PBDC=S△BDC+S△APC=BC×PD，建立函数关系式，求出极值即可；

（3）先判断出PE=CE，再得到∠PCE=∠DBE，以C、P、Q为顶点的三角形与△ABC相似，分两种情况计算即可．

本题解析：

(1)将点A(9,10)代入得：81a18+1=10，

解得：a=，

∴抛物线解析式为y=x2x+1，

当x=0时,y=1,即点B(0,1)，

∵抛物线对称轴为x=3，

∴点B关于对称轴的对称点C坐标为(6,1)，

故答案为：y=x2x+1,(0,1),(6,1)；

(2)如图2，

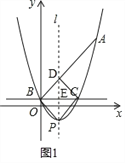
设直线AB的解析式为y=kx+b，

将A(9,10)、B(0,1)代入得： ，

解得： ，

∴直线AB的解析式为y=x+1，

设点P(m, m2m+1)

∴D(m,m+1)

∴PD=m+1(m2m+1)= m+3m，

∵BC⊥PD，BC=6，

∴S四边形PBDC=S△BDC+S△APC=BC×DE+12BC×PE=BC(DE+PE)= BC×PD=×6×(m+3m)=m+9m=(m)+，

∵0<m<6，

∴当m=时,四边形PBDC的面积取得最大值，

此时点P的坐标为(,；

(3)如图2，

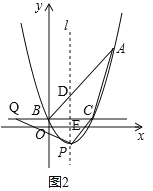
∵y=x2x+1= (x3)2，

∴P(3,2)，

∴PE==3,CE==3，

∴PE=CE，

∴∠PCE=45°

同理可得：∠DBE=45°，

∴∠PCE=∠DBE，

∴在直线AC上存在满足条件的Q，

设Q(t,1)且AB=9,BC=6,CP=3,

∵以C. P、Q为顶点的三角形与△ABC相似，

①当△CPQ∽△BAC时，

∴，

∴，

∴t=4，

∴Q(4,1)

②当△CPQ∽△BCA时，

∴，

∴，

∴t=3，

∴Q(3,1)，

综上,点Q的坐标为(4,1)或(3,1).