题目内容
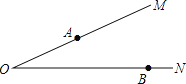
【题目】如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
A.3 B.3![]() C.2 D.2
C.2 D.2![]()
【答案】D
【解析】
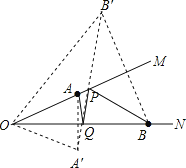
试题分析:首先作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,可求得AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,然后由特殊角的三角函数值,判定∠OA′B′=90°,再利用勾股定理求得答案.
解:作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,
则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°,
∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,
∵cos60°=![]() ,
,![]() =
=![]() ,
,
∴∠OA′B′=90°,
∴A′B′=![]() =2
=2![]() ,
,
∴线段AQ+PQ+PB的最小值是:2![]() .
.
故选D.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目