题目内容
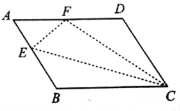
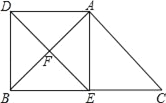
【题目】如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ACED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由已知可得:EF是△ABC的中位线,则可得EF∥AB,EF=![]() AB,又由DF=EF,易得AB=DE,根据有一组对边平行且相等的四边形是平行四边形,即可证得四边形ABED是平行四边形;
AB,又由DF=EF,易得AB=DE,根据有一组对边平行且相等的四边形是平行四边形,即可证得四边形ABED是平行四边形;
(2)由(1)可得四边形AECD是平行四边形,又由AB=AC,AB=DE,易得AC=DE,根据对角线相等的平行四边形是矩形,可得四边形AECD是矩形.
试题解析:(1)∵E、F分别为△ABC的边BC、CA的中点,
∴EF∥AB,EF=![]() AB,
AB,
∵DF=EF,
∴EF=![]() DE,
DE,
∴AB=DE,
∴四边形ABED是平行四边形;
(2)∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,
∵AB=AC,AB=DE,
∴AC=DE,
∴四边形AECD是矩形.
或∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,
∵AB=AC,BE=EC,
∴∠AEC=90°,
∴四边形AECD是矩形.

练习册系列答案
相关题目