Question

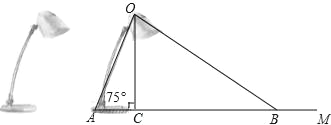
【题目】如图（1），在Rt△ABC，∠ACB＝90°，分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M．

（1）求证：△ABD≌△FBC；

（2）如图（2），求证：AM2+MF2＝AF2．

Answer 1

【答案】（1）证明见详解；（2）证明见详解

【解析】

（1）根据四边形ABFG、BCED是正方形得到两对边相等，一对直角相等，根据图形利用等式的性质得到一对角相等，利用SAS即可得到三角形全等；
（2）根据全等三角形的性质和勾股定理即可得到结论．

解：（1）∵四边形ABFG、BCED是正方形，
∴AB=FB，CB=DB，∠ABF=∠CBD=90°，
∴∠ABF+∠ABC=∠CBD+∠ABC，
即∠ABD=∠CBF，
在△ABD和△FBC中，

，
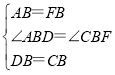∴△ABD≌△FBC（SAS）；
（2）∵△ABD≌△FBC，
∴∠BAD=∠BFC，
∴∠AMF=180°-∠BAD-∠CNA=180°-（∠BFC+∠BNF）=180°-90°=90°，
∴AM2+MF2=AF2．