题目内容
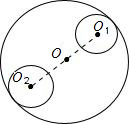
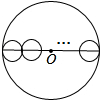 如图,大圆内有n个圆心都在大圆直径上的小圆,从左到右,大圆和第一个小圆内切,第一个小圆与第二个小圆外切,第二个小圆与第三个小圆处切,…依此类推,第n个小圆与大圆内切.若大圆半径为1,则这n个小圆的周长和为( )
如图,大圆内有n个圆心都在大圆直径上的小圆,从左到右,大圆和第一个小圆内切,第一个小圆与第二个小圆外切,第二个小圆与第三个小圆处切,…依此类推,第n个小圆与大圆内切.若大圆半径为1,则这n个小圆的周长和为( )分析:根据题干:一个半径为1的大圆内有许多小圆,这些小圆的圆心都在大圆的一个直径上,可知大圆的直径等于所有小圆的直径之和.根据圆周长公式可解决.
解答:解:每个小圆的半径未知,但所有小圆直径加起来正好是大圆的直径.
大圆半径为1,小圆直径为r1,r2,r3…,
大圆周长C=2π,
小圆周长之和=2πr1+2πr2+2πr3…=2πr=2π;
所以所有小圆的周长之和等于大圆周长,
答:所有小圆周长之和是2π.
故选B.
大圆半径为1,小圆直径为r1,r2,r3…,
大圆周长C=2π,
小圆周长之和=2πr1+2πr2+2πr3…=2πr=2π;
所以所有小圆的周长之和等于大圆周长,
答:所有小圆周长之和是2π.
故选B.
点评:此题属于较复杂的圆周长的计算,解决本题的关键是所有的小圆的圆心都在大圆的一条直径上,即所有小圆的直径之和等于大圆的直径,理解了这一点,此题就非常简单了.

练习册系列答案
相关题目
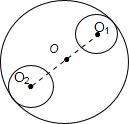
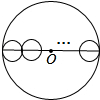 如图,大圆内有n个圆心都在大圆直径上的小圆,从左到右,大圆和第一个小圆内切,第一个小圆与第二个小圆外切,第二个小圆与第三个小圆处切,…依此类推,第n个小圆与大圆内切.若大圆半径为1,则这n个小圆的周长和为
如图,大圆内有n个圆心都在大圆直径上的小圆,从左到右,大圆和第一个小圆内切,第一个小圆与第二个小圆外切,第二个小圆与第三个小圆处切,…依此类推,第n个小圆与大圆内切.若大圆半径为1,则这n个小圆的周长和为