题目内容
【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
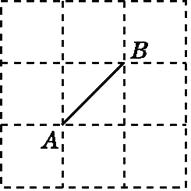
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°,![]() =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
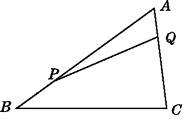
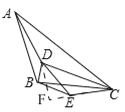
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.

【答案】(1)证明见解析;(2)n=![]() ;(3)c2﹣b2=(2+
;(3)c2﹣b2=(2+![]() )a2,理由见解析.
)a2,理由见解析.
【解析】试题分析:(1)先判断出△ABC∽△DEC,得出![]() ,即可得出结论;
,即可得出结论;
(2)先求出AC=![]() BC,同理:CD=
BC,同理:CD=![]() EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD=
EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD=![]() BE,BE=
BE,BE=![]() ,再利用勾股定理得出DE2=
,再利用勾股定理得出DE2=![]() 再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;
再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;
(3)同(2)的方法![]() ,再构造直角三角形,利用勾股定理即可得出结论.
,再构造直角三角形,利用勾股定理即可得出结论.
试题解析:(1)∵△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,
∴△ABC∽△DEC,
∴![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵![]() ,
,
∴△ACD∽△BCE;
(2)在Rt△ABC中,AC=![]() =
=![]() BC,
BC,
同理:CD=![]() EC,
EC,
∵∠ABC=∠DEC=90°,
∵![]() ,
,
∴![]()
∴△ABC∽△DEC,
∴![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵![]() ,
,
∴△ACD∽△BCE,
∴![]() =
=![]() ,
,
∴AD=![]() BE,
BE,
∵AD=2,
∴BE=![]() ,
,
在Rt△CDE中,CD2=DE2+CE2=(n2+1)CE2=9,
∴CE2=![]()
∴DE2=n2CE2=n2×![]() =
=![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2=1+![]() ,
,
∴![]() =1+
=1+![]() ,
,
∴n=﹣![]() (舍)或n=
(舍)或n=![]() ;
;
(3)c2﹣b2=(2+![]() )a2,
)a2,
理由:如图,∵AB=BC,DE=EC,
∴![]() ,
,
∵∠ABC=∠DEC,
∴△ABC∽△DEC,
∴![]() ,
,
∵AB=BC,DE=EC,且∠ABC=∠DEC=135°,
∴∠ACB=∠DCE=22.5°,
∴∠ACD=∠BCE,
∵![]() ,
,
∴△ACD∽△BCE,
∴![]() ,
,
∴![]() ,
,
过点D作DF⊥CE交CE的延长线于F,
∵∠DEC=135°,
∴∠DEF=45°,
设DF=x,
∴EF=x,DE=![]() x,
x,
∵EC=DE=![]() x,
x,
∴CF=EF+EC=(![]() +1)x,
+1)x,
在Rt△CDF中,CF2+DF2=CD2,
∴[(![]() +1)x]2+x2=c2,
+1)x]2+x2=c2,
∴x2=![]() ,
,
∴DE2=2x2=![]() ,
,
∴BE2=![]() =
=![]() ×
×![]() =
=![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2,
∴![]() =a2+
=a2+![]() ,
,
∴c2﹣b2=(2+![]() )a2.
)a2.

 名校课堂系列答案
名校课堂系列答案