题目内容
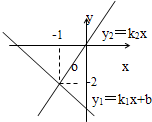如图所示，两函数y1=k1x+b和y2=k2x的图象相交于点（-1，-2），则关于x的不等式 k1x+b＞k2x的解集为
- A.x＞-1
- B.x＜-1
- C.x＜-2
- D.无法确定
B
分析：由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式k1x+b＞k2x解集．
解答：两个条直线的交点坐标为（-1，-2），
当x＞-1时，直线y1在直线y2的上方，
故不等式k1x+b＞k2x的解集为：x＜-1．
故选：B．
点评：此题主要考查了利用一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．
分析：由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式k1x+b＞k2x解集．
解答：两个条直线的交点坐标为（-1，-2），
当x＞-1时，直线y1在直线y2的上方，
故不等式k1x+b＞k2x的解集为：x＜-1．
故选：B．
点评：此题主要考查了利用一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．
练习册系列答案
相关题目
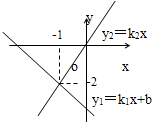如图所示，两函数y1=k1x+b和y2=k2x的图象相交于点（-1，-2），则关于x的不等式 k1x+b＞k2x的解集为（ ）
和y2＝
(mn≠0)相交于A，C两点，若Rt△OCD的面积是Rt△OAB的面积的两倍，问点P(m，n)是否在函数y＝－2x上？说明理由．
