题目内容
如图,二次函数 的图象经过点D,与x轴交于A、B两点。
的图象经过点D,与x轴交于A、B两点。
 的图象经过点D,与x轴交于A、B两点。
的图象经过点D,与x轴交于A、B两点。
(1)求c的值;
(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
(3)设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由。(图②供选用)
(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
(3)设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由。(图②供选用)
解:(1)∵抛物线经过点D(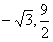 )
)
∴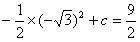
∴c=6。
(2)过点D、B点分别作AC的垂线,垂足分别为E、F,设AC与BD交点为M,
∵AC 将四边形ABCD的面积二等分,即:S△ABC=S△ADC
∴DE=BF
又∵∠DME=∠BMF,∠DEM=∠BFE
∴△DEM≌△BFM
∴DM=BM
即AC平分BD
∵c=6
∵抛物线为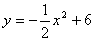
∴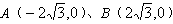
∵M是BD的中点
∴
设AC的解析式为y=kx+b,经过A、M点
∴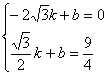
解得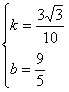
∴直线AC的解析式为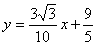 。
。
(3)存在.设抛物线顶点为N(0,6),在Rt△AQN中,易得AN=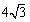 ,于是以A点为圆心,AB=
,于是以A点为圆心,AB=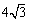 为半径作圆与抛物线在x上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP、PQ,此时由“边角边”易得△AQP≌△ABP。
为半径作圆与抛物线在x上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP、PQ,此时由“边角边”易得△AQP≌△ABP。
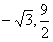 )
)∴
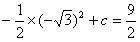
∴c=6。
(2)过点D、B点分别作AC的垂线,垂足分别为E、F,设AC与BD交点为M,
∵AC 将四边形ABCD的面积二等分,即:S△ABC=S△ADC
∴DE=BF
又∵∠DME=∠BMF,∠DEM=∠BFE
∴△DEM≌△BFM
∴DM=BM
即AC平分BD
∵c=6
∵抛物线为
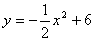
∴
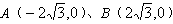
∵M是BD的中点
∴

设AC的解析式为y=kx+b,经过A、M点
∴
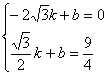
解得
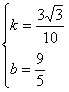
∴直线AC的解析式为
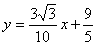 。
。(3)存在.设抛物线顶点为N(0,6),在Rt△AQN中,易得AN=
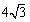 ,于是以A点为圆心,AB=
,于是以A点为圆心,AB=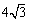 为半径作圆与抛物线在x上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP、PQ,此时由“边角边”易得△AQP≌△ABP。
为半径作圆与抛物线在x上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP、PQ,此时由“边角边”易得△AQP≌△ABP。
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).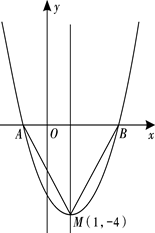
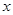 轴的交点A,B的坐标;
轴的交点A,B的坐标; 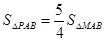 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;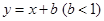 与此图象有两个公共点时,
与此图象有两个公共点时,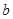 的取值范围.
的取值范围.