题目内容
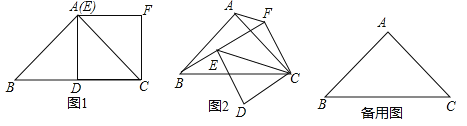
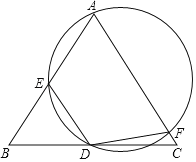
【题目】如图,在△ABC中,AB=AC,点D为BC的中点,经过AD两点的圆分别与AB,AC交于点E、F,连接DE,DF.
(1)求证:DE=DF;
(2)求证:以线段BE+CF,BD,DC为边围成的三角形与△ABC相似,
【答案】(1)详见解析;(2)详见解析
【解析】
(1)连接AD,证明∠BAD=∠CAD即可得出![]() ,则结论得出;
,则结论得出;
(2)在AE上截取EG=CF,连接DG,证明△GED≌△CFD,得出DG=CD,∠EGD=∠C,则可得出结论△DBG∽△ABC.
(1)证明:连接AD,

∵AB=AC,BD=DC,
∴∠BAD=∠CAD,
∴![]() ,
,
∴DE=DF.
(2)证明:在AE上截取EG=CF,连接DG,

∵四边形AEDF内接于圆,
∴∠DFC=∠DEG,
∵DE=DF,
∴△GED≌△CFD(SAS),
∴DG=CD,∠EGD=∠C,
∵AB=AC,
∴∠B=∠C,
∴△DBG∽△ABC,
即以线段BE+CF,BD,DC为边围成的三角形与△ABC相似.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目