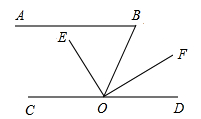
题目内容
已知直线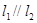 ,直线
,直线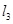 与
与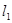 、
、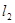 分别交于
分别交于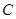 、
、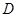 两点,点
两点,点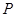 是直线
是直线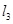 上的一动点
上的一动点
如图,若动点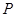 在线段
在线段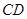 之间运动(不与
之间运动(不与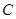 、
、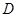 两点重合),问在点
两点重合),问在点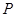 的运动过程中是否始终具有
的运动过程中是否始终具有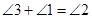 这一相等关系?试说明理由;
这一相等关系?试说明理由;
如图,当动点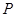 在线段
在线段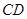 之外且在的上方运动(不与
之外且在的上方运动(不与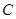 、
、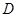 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
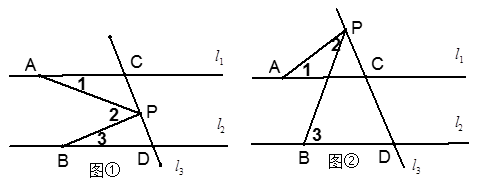
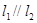 ,直线
,直线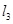 与
与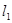 、
、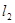 分别交于
分别交于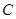 、
、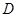 两点,点
两点,点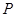 是直线
是直线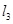 上的一动点
上的一动点如图,若动点
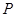 在线段
在线段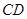 之间运动(不与
之间运动(不与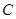 、
、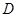 两点重合),问在点
两点重合),问在点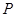 的运动过程中是否始终具有
的运动过程中是否始终具有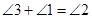 这一相等关系?试说明理由;
这一相等关系?试说明理由;如图,当动点
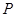 在线段
在线段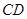 之外且在的上方运动(不与
之外且在的上方运动(不与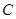 、
、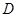 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;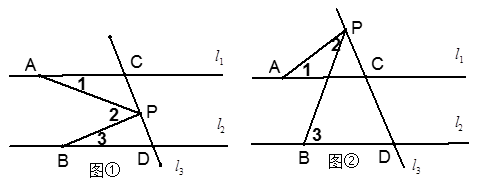
(1)∠3+∠1=∠2成立,理由见解析;(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2.
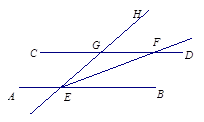
试题分析:(1)相等关系成立.过点P作PE∥l1,则有∠1=∠APE,又因为PE∥l2,又有∠3=∠BPE,因为∠BPE+∠APE=∠2,所以∠3+∠1=∠2;
(2)原关系不成立,过点P作PE∥l1,则有∠1=∠APE;又因为PE∥l2,又有∠3=∠BPE,困为此时∠BPE-∠APE=∠2,则有∠3-∠1=∠2.
(1)∠3+∠1=∠2成立.
理由如下:
过点P作PE∥l1,
∴∠1=∠APE;
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE;
又∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2.

(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2.
理由如下:
过点P作PE∥l1,
∴∠1=∠APE;
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE;
又∵∠BPE-∠APE=∠2,
∴∠3-∠1=∠2.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
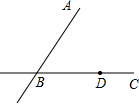


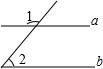
 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是