题目内容
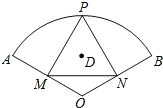
【题目】如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长 ( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】B
【解析】根据题意画出点N离开点O时,到点M到达点O时的图形,得到点D运动的轨迹是点O为圆心,以2为半径,圆心角为60°的弧,根据弧长公式计算即可.
解:当点N与点O重合时,∠P′OA=30°,OD=![]() OP′=2,
OP′=2,
当点M与点O重合时,∠P′′OB=30°,OD=![]() OP′′=2,
OP′′=2,
∴∠P′OA P′′=60°
∵D是△PMN的外心,
∴点D在线段PM的垂直平分线上,又PM⊥OA,
∴D为OP的中点,即OD=![]() OP=2,
OP=2,
∴点D运动的轨迹是以点O为圆心,2为半径,圆心角为60°的弧,
弧长为:![]() .
.
故选:B.
点晴:本题主要考查的是弧长的计算,要求学生掌握弧长的计算公式![]() ,并能够在动态的图形中寻找到图形的变化规律,而根据题意确定点D的运动轨迹是解题的关键.要想理解点D的运动轨迹,就要先从P的起始位置和终止位置这两个特殊位置进行观察,从而可得出点D运动的轨迹是以点O为圆心,2为半径,圆心角为60°的弧.
,并能够在动态的图形中寻找到图形的变化规律,而根据题意确定点D的运动轨迹是解题的关键.要想理解点D的运动轨迹,就要先从P的起始位置和终止位置这两个特殊位置进行观察,从而可得出点D运动的轨迹是以点O为圆心,2为半径,圆心角为60°的弧.

练习册系列答案
相关题目