��Ŀ����
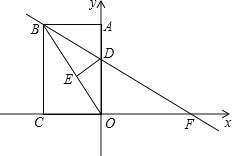
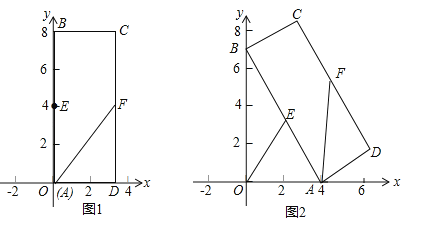
����Ŀ������ABCD�У���C��3��8����E��FΪAB��CD���ϵ��е㣬��ͼ1����A��ԭ�㴦����B��y���������ϣ���C�ڵ�һ���ޣ�����A��ԭ���������x��������ÿ��1����λ���ȵ��ٶ��˶�����B��֮��y���»�������������ABCD��ƽ���ڻ�������ͼ2�����˶�ʱ���ʾΪt�룬����B����ԭ��ʱֹͣ�˶���
��1����t=0ʱ����F������Ϊ ��
��2����t=4ʱ����OE�ij�����B�»��ľ��룻
��3�����˶������У���F����O�������룻
��4�����Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ����t��ֵ��
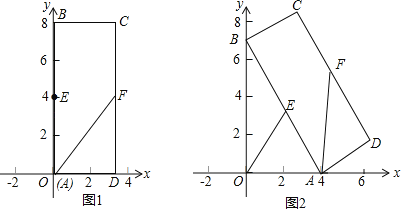
���𰸡���1��F��3��4������2��8-![]() ����3��7����4��t��ֵΪ
����3��7����4��t��ֵΪ![]() ��
��![]() .
.
�������������������1����ȷ����DF�������ó���F��������
��2������ֱ�������ε����ʵó���ABO=30�㣬���ɵó�������
��3����O��E��F���㹲��ʱ����F����O�ľ�����������ɵó�������
��4��������������������������ε����ʽ���������⼴�ɣ�
���������������1����t=0ʱ����AB=CD=8��FΪCD�е�����DF=4����F��3��4����
��2����t=4ʱ��OA=4����Rt��ABO����AB=8����AOB=90�㣬
���ABO=30�㣬��E��AB���е���OE=![]() AB=4��BO=
AB=4��BO=![]() �����B�»��ľ���Ϊ
�����B�»��ľ���Ϊ![]() ��
��
��3����O��E��F���㹲��ʱ����F����O�ľ����������FO=OE+EF=7��
��4����Rt��ADF����FD2+AD2=AF2����AF=![]() =5������AO=t1ʱ����F��x����������AΪ�е�����FA��OA�����OAB+��FAB=90�㣮�ߡ�FAD+��FAB=90�㣬���BAO=��FAD���ߡ�BOA=��D=90�㣬��Rt��FAE��Rt��ABO����
=5������AO=t1ʱ����F��x����������AΪ�е�����FA��OA�����OAB+��FAB=90�㣮�ߡ�FAD+��FAB=90�㣬���BAO=��FAD���ߡ�BOA=��D=90�㣬��Rt��FAE��Rt��ABO����![]() ����
����![]() ����t1=
����t1=![]() ������AO=t2ʱ����F��y��������BΪ�е���ͬ���ɵ���t2=
������AO=t2ʱ����F��y��������BΪ�е���ͬ���ɵ���t2=![]() ��
��
�������������Ե�FΪԲ����FAΪ�뾶��Բ������������ʱ��t��ֵΪ![]() ��
��![]() ��
��

����Ŀ��ij��˾�ƻ�Ͷ��50��Ԫ�������������������ֲ�Ʒ�������г�����Ԥ�Ƽײ�Ʒ�������y1����Ԫ����Ͷ���ʽ�x����Ԫ�������������Ҳ�Ʒ�������y2����Ԫ����Ͷ���ʽ�x����Ԫ����ƽ��������������ù�˾Ͷ���Ҳ�Ʒx����Ԫ�������ֲ�Ʒ�����ܻ���Ϊy��Ԫ��x��0�����õ��˱��е����ݣ�
x����Ԫ�� | 20 | 30 |
y����Ԫ�� | 10 | 13 |
��1����y��x�ĺ�����ϵʽ��
��2���ù�˾���ٿɻ�ö�����������������ѧ����ѧ֪ʶ�Ըù�˾Ͷ���ʽ�ķ��������������
�飬ʹ���ܻ��������������������Ƕ��٣�
��3��������������۳�Ͷ���Ҳ�Ʒ�ʽ��a����a��1����ʣ��������x�������С����a��ȡֵ
����