题目内容
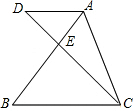如图，线段AB、CD相交于E，AD∥BC，若AE：EB=1：2，S△ADE=1，则S△AEC等于分析：由AD∥BC，利用平行线分线段成比例定理，即可得DE：EC=1：2，又由△ADE与△AEC等高，根据等高三角形的面积比等于对应底的比，即可求得答案．
解答：解：∵AD∥BC，
∴
=
=
，
∴
=
=
，
∵S△ADE=1，
∴S△AEC=2．
∴
| AE |
| EB |
| DE |
| EC |
| 1 |
| 2 |
∴
| S△ADE |
| S△AEC |
| DE |
| EC |
| 1 |
| 2 |
∵S△ADE=1，
∴S△AEC=2．
点评：此题考查了平行线分线段成比例定理与三角形面积的求解方法．此题难度适中，解题的关键是注意数形结合思想的应用．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
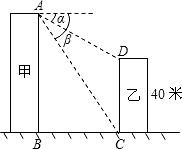如图，线段AB，CD分别表示甲、乙两建筑物的高，AB⊥BC，CD⊥BC，从A点测得D点的俯角α为30°，测得C点的俯角β为60°，已知乙建筑物高CD=40米．试求甲建筑物高AB．
11、如图，线段AB=BC=CD=DE=1厘米，那么图中所有线段的长度之和等于
6、如图，线段AB、CD互相平分于点O，过O作EF交AC于E，交BD于F，则这个图形是中心对称图形，对称中心是O．指出图形中的对应点
当两车油箱中剩余油量相同时，那么两车的行驶路程相差多少千米？