题目内容
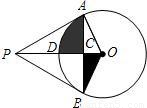
(2009•南宁)如图,PA、PB是半径为1的⊙O的两条切线,点A、B分别为切点,∠APB=60°,OP与弦AB交于点C,与⊙O交于点D.(1)在不添加任何辅助线的情况下,写出图中所有的全等三角形;
(2)求阴影部分的面积(结果保留π).
【答案】分析:(1)中根据圆的切线的性质及对称性,可确定图中的全等三角形;
(2)阴影部分的面积可转化为扇形面积从而利用公式进行计算.
解答:解:(1)△ACO≌△BCO,△APC≌△BPC,△PAO≌△PBO;
(2)∵PA、PB为⊙O的切线,
∴PO平分∠APB,PA=PB,∠PAO=90°,
∴PO⊥AB,(6分)
∴由圆的对称性可知:S阴影=S扇形AOD,
∵在Rt△PAO中,∠APO= ∠APB=
∠APB= ×60°=30°,
×60°=30°,
∴∠AOP=90°-∠APO=90°-30°=60°,
∴S阴影=S扇形AOD=
= .
.
点评:主要考查了圆的对称性和扇形的面积公式.
(2)阴影部分的面积可转化为扇形面积从而利用公式进行计算.
解答:解:(1)△ACO≌△BCO,△APC≌△BPC,△PAO≌△PBO;
(2)∵PA、PB为⊙O的切线,
∴PO平分∠APB,PA=PB,∠PAO=90°,
∴PO⊥AB,(6分)
∴由圆的对称性可知:S阴影=S扇形AOD,
∵在Rt△PAO中,∠APO=
 ∠APB=
∠APB= ×60°=30°,
×60°=30°,∴∠AOP=90°-∠APO=90°-30°=60°,
∴S阴影=S扇形AOD=

=
 .
.点评:主要考查了圆的对称性和扇形的面积公式.

练习册系列答案
相关题目
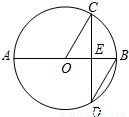 (2009•南宁)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为
(2009•南宁)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为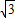 cm,则弦CD的长为( )
cm,则弦CD的长为( ) cm
cm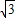 cm
cm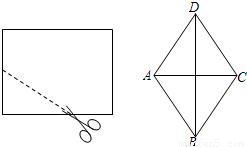
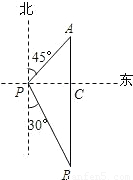
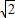 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为 海里(结果保留根号).
海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为 海里(结果保留根号).