题目内容
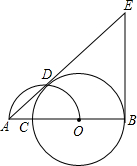 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E.
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E.(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长时关于x的方程x2-kx+4
| 5 |
(3)当点O位于线段AB何处时,△ODC恰好是等边三角形?并说明理由.
分析:(1)连接OD.只需证明OD⊥AE即可;
(2)根据两根之积求得AD的长,再根据切割线定理求得AB的长,再根据△AOD∽△AEB即可求解;
(3)要探索△ODC恰好是等边三角形,则OB=OC,即点O是AB的中点,再进一步反过来证明.
(2)根据两根之积求得AD的长,再根据切割线定理求得AB的长,再根据△AOD∽△AEB即可求解;
(3)要探索△ODC恰好是等边三角形,则OB=OC,即点O是AB的中点,再进一步反过来证明.
解答: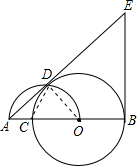 (1)证明:连接OD.
(1)证明:连接OD.
根据直径所对的圆周角是直角,得OD⊥AE,
则AE切⊙O于点D.
(2)解:∵AC=2,AC、AD是所给方程的两根,
∴2AD=4
,
∴AD=2
.
由切割线定理,得AD2=AC•AB,
∴AB=
=10,
则BC=AB-AC=10-2=8,
∴OD=4.
在△AOD和△AEB中,∵∠A=∠A,
又∵EB⊥AB,
∴∠EBA=∠ODA=90°
∴△AOD∽△AEB.
∴
=
,
∴BE=
=4
.
(3)解:当点O位于线段AB上靠近B的三等分点处时,△ODC恰好为等边三角形.
证明如下:∵OB=OC=
BC,
∴AC=
AB.
∴AC=OC=OD.
∴C为以AO为直径的圆的圆心.
∴CD=OC=OD.
∴△ODC是等边三角形.
 (1)证明:连接OD.
(1)证明:连接OD.根据直径所对的圆周角是直角,得OD⊥AE,
则AE切⊙O于点D.
(2)解:∵AC=2,AC、AD是所给方程的两根,
∴2AD=4
| 5 |
∴AD=2
| 5 |
由切割线定理,得AD2=AC•AB,
∴AB=
| AD2 |
| AC |
则BC=AB-AC=10-2=8,
∴OD=4.
在△AOD和△AEB中,∵∠A=∠A,
又∵EB⊥AB,
∴∠EBA=∠ODA=90°
∴△AOD∽△AEB.
∴
| OD |
| BE |
| AD |
| AB |
∴BE=
| OD•AB |
| AD |
| 5 |
(3)解:当点O位于线段AB上靠近B的三等分点处时,△ODC恰好为等边三角形.
证明如下:∵OB=OC=
| 1 |
| 2 |
∴AC=
| 1 |
| 3 |
∴AC=OC=OD.
∴C为以AO为直径的圆的圆心.
∴CD=OC=OD.
∴△ODC是等边三角形.
点评:此题综合运用了圆周角定理的推论、相似三角形的判定和性质、切割线定理以及等边三角形的判定和性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
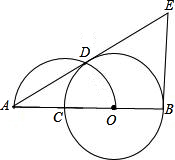 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;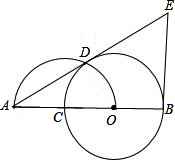 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;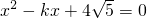 的两根,求线段EB的长.
的两根,求线段EB的长.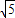 =0的两根,求线段EB的长;
=0的两根,求线段EB的长;
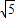 =0的两根,求线段EB的长;
=0的两根,求线段EB的长;