题目内容
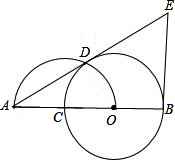 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长是关于x的方程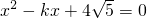 的两根,求线段EB的长.
的两根,求线段EB的长.
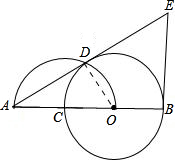 (1)证明:连接OD.
(1)证明:连接OD.∵AO为半圆直径,∴∠ADO=90°.
∴AE切⊙O于点D;
(2)∵AC、AD的长是关于x的方程
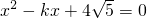 的两根,
的两根,∴AC•AD=4
 ;
;∵AC=2,
∴AD=2
 .
.设OD=OC=x,则(x+2)2=(2
 )2+x2.
)2+x2.解得x=4.
∴AB=2+8=10.
∵∠ADO=∠ABE=90°,∠A=∠A,
∴△AOD∽△AEB,
∴
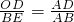 ,即
,即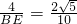 ,
,∴BE=4
 .
.分析:(1)连接OD,证明OD⊥AD即可.由AD是半圆直径易证;
(2)根据题意,AC•AD=4
 ,则AD=2
,则AD=2 .在Rt△AOD中利用勾股定理可求半径,知△AOD各边的长度.
.在Rt△AOD中利用勾股定理可求半径,知△AOD各边的长度.证明△AOD∽△AEB,得比例线段建立已知和未知之间的联系求解.
点评:此题考查了切线的判定、相似三角形的判定和性质等知识点,综合性强,难度中上.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
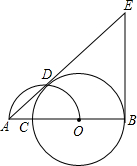 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E.
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E.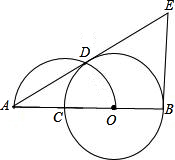 如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;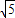 =0的两根,求线段EB的长;
=0的两根,求线段EB的长;
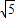 =0的两根,求线段EB的长;
=0的两根,求线段EB的长;