Question

5、正方形OABC在平面直角坐标系中的位置如图，点B（2，0），点A、C关于x轴对称，则点C的坐标为（　　）

A、（1，1）

B、（1，-1）

C、（-1，1）

D、（-1，-1）

Answer 1

分析：AC在BO的垂直平分线上，即AC的横坐标和OB中点横坐标相等，根据正方形对角线计算求A、C的纵坐标．

解答：解：

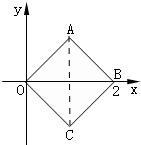
连接AC，则AC所在直线为OB的垂直平分线，即A、C的横坐标均为1，
根据正方形对角线相等的性质，AC=BO=2，
∵A、C关于x轴对称，
∴A点纵坐标为1，C点纵坐标为-1，
故C点坐标（1，-1），
故选择B．

点评：本题考查了正方形对角线互相垂直平分且相等的性质，根据对角线相等的性质求对角线AC的长度，即A、C的纵坐标是解题的关键．