题目内容
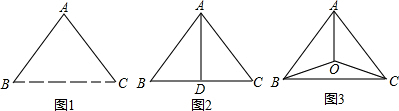
已知如图,边长为2的正方形OABC在平面直角坐标系中,位于x轴上方,与x轴的正半轴的夹角为![]() ,则B点的坐标为
,则B点的坐标为

[ ]
A.( -2,
-2, +1)
+1)
B.( +1,
+1, -2)
-2)
C.(1- ,
, +1)
+1)
D.(1+ ,1-
,1- )
)
答案:C
解析:
解析:
|
如图,作CD⊥y轴于点D,BE⊥CD于点E. ∠AOD=90°-60°=30°,∠COD=∠AOC-∠AOD=60°. 在Rt△OCD中,∠OCD=90°-∠COD=30°,OD=OC·cos∠COD=1,CD=OC·sin∠COD= 在Rt△BCE中,CE=BC·cos∠BCE=1,BE=BC·sin∠BCE= 则OF=DE=CD-CE= ∴B(1-
|

练习册系列答案
相关题目
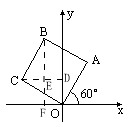

 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P. (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.