题目内容
【题目】如图所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=°,∠D=°,∠E=°.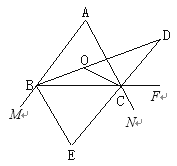
【答案】120;30;60
【解析】∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×120°=60°,
×120°=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
∵∠ACF是△ABC的外角,∠ABC的内角平分线与∠ACB的外角平分线交于点D,
∴∠DCF= ![]() ∠ACF =
∠ACF = ![]() (∠ABC+∠A)=∠CBD+
(∠ABC+∠A)=∠CBD+ ![]() ∠A,
∠A,
∴∠D=∠DCF-∠CBD= ![]() ∠A=30;
∠A=30;
∵∠CBM,∠BCN是△ABC的外角,
∴∠CBM+∠BCN=(∠A+∠ACB)+(∠A+∠ABC)=180°+∠A.
∵∠ABC与∠ACB的相邻外角平分线交于点E,
∴∠CBE+∠BCE= ![]() (∠CBM +∠BCN)=90°+
(∠CBM +∠BCN)=90°+ ![]() ∠A,
∠A,
∴∠E=180-(∠CBE+∠BCE)=90°- ![]() ∠A=60°.
∠A=60°.
【考点精析】通过灵活运用三角形的外角,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.

练习册系列答案
相关题目