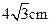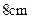题目内容
在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F;
求证:DF=DC.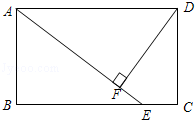
根据矩形的性质和DF⊥AE于F,可以得到∠DEC=∠AED,∠DFE=∠C=90,进而依据AAS可以证明
△DFE≌△DCE.然后利用全等三角形的性质解决问题。
解析分析:根据矩形的性质和DF⊥AE于F,可以得到∠DEC=∠AED,∠DFE=∠C=90,进而依据AAS可以证明
△DFE≌△DCE.然后利用全等三角形的性质解决问题。
证明:连接DE,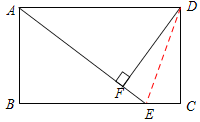
∵AD=AE,∴∠AED=∠ADE。
∵矩形ABCD,∴AD∥BC,∠C=90°。
∴∠ADE=∠DEC。∴∠DEC=∠AED。
又∵DF⊥AE,∴∠DFE=∠C=90°。
∵DE=DE,∴△DFE≌△DCE(AAS)。
∴DF=DC。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

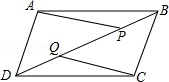
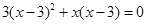
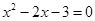 (用配方法解)
(用配方法解)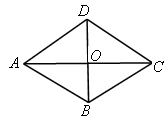
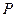 的距离是( )
的距离是( )