Question

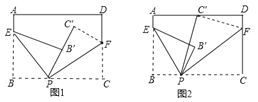
【题目】如图所示，边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合．

(1)旋转中心是哪一点?

(2)四边形A′B′C′D′，是怎样的图形?面积是多少?

(3)求∠C′DC和∠CDA′的度数；

(4)连接AA′，求∠DAA′的度数．

Answer 1

【答案】（1）点D（2）边长为4的正方形，16（3）30°，60°（4）75°

【解析】试题分析：（1）根据题意可得旋转中心是D点；

（2）因为四边形A′B′C′D′是由正方形ABCD旋转得到的，所以它是和四边形ABCD全等的正方形，边长还是4；

（3）根据旋转的宗旨即可得到；

（4）根据等腰三角形的性质即可求解.

试题解析：(1)旋转中心是点D.

(2)四边形A′B′C′D′是正方形，旋转不改变图形的大小，四边形A′B′C′D′是正方形ABCD旋转得来的，而正方形ABCD的面积为16，所以四边形A′B′C′D′的面积是16．

(3)因为C与C′是对应点，而对应点与旋转中心连线所成的角即是旋转角，由题意知图形绕点D旋转30°，所以∠C′DC＝30°．又因为四边形A′B′C′D′是正方形，所以∠C′DA′＝90°，而∠C′DC＝30°，所以∠CDA′＝60°．

(4)根据旋转的特征，对应点到旋转中心的距离相等，所以由点D，A，A′所确定的三角形是等腰三角形，AD＝A′D，而∠ADA′＝30°，所以∠DAA′＝∠DA′A＝（180°-30°）÷2=75°.