题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 角,得到
角,得到![]() 矩形,
矩形,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() .
.
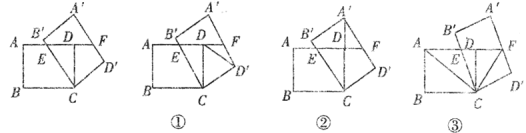
(1)如图①,当![]() 时,连接
时,连接![]() ,求
,求![]() 和
和![]() 的长;
的长;
(2)如图②,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 的延长线上时,求
的延长线上时,求![]() 的长;
的长;
(3)如图③,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①如图①中,由矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',只要证明△CDD′是等边三角形即可解决问题;
②如图①中,连接CF,在Rt△CD′F中,求出FD′即可解决问题;
(2)由△A′DF∽△A′D′C,可得![]() ,推出
,推出![]() 同理可得△CDE∽△CB′A′,由
同理可得△CDE∽△CB′A′,由![]() 求出DE,即可解决问题;
求出DE,即可解决问题;
(3)如图③中,作FG⊥CB′于G,由![]() 把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
解析:(1)①如图①中,
![]() 矩形
矩形![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 角,得到矩形
角,得到矩形![]() ,
,
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
②如图①中,连接![]() .
.![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
(2)如图②中,在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
同理可得,![]()
![]()
![]()
![]()
![]()
(3)如图③中,作![]() 于
于![]() ,
,![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目
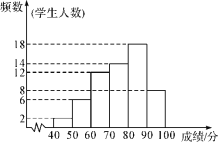
【题目】在画二次函数![]() 的图象时,甲写错了一次项的系数,列表如下
的图象时,甲写错了一次项的系数,列表如下
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 3 | 2 | 3 | 6 | …… |
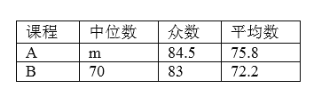
乙写错了常数项,列表如下:
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | ﹣2 | ﹣1 | 2 | 7 | 14 | …… |
通过上述信息,解决以下问题:
(1)求原二次函数![]() 的表达式;
的表达式;
(2)对于二次函数![]() ,当
,当![]() _____时,
_____时,![]() 的值随
的值随![]() 的值增大而增大;
的值增大而增大;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围.
的取值范围.