题目内容
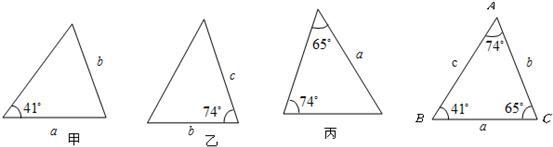
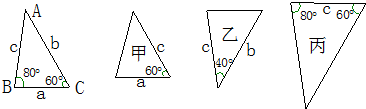
如图,下面甲、乙、丙三个三角形中和△ABC全等的图形是
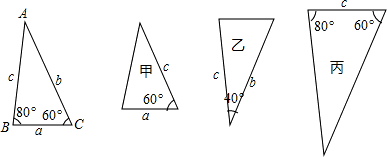
- A.只有甲
- B.只有乙
- C.只有丙
- D.甲乙丙都是
B
分析:根据全等三角形的判定定理作出判断与选择.
解答:在△ABC中,∠A=40°.
甲:只有一个对应边与一个对应角相等,故甲不符合条件;
乙:由两个对应边与这两个边的夹角相等,符合两个三角形全等的定理SAS;
丙:两个角对应相等,但是这两个角间的线段不相等,故丙不符合条件.
故选B.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
分析:根据全等三角形的判定定理作出判断与选择.
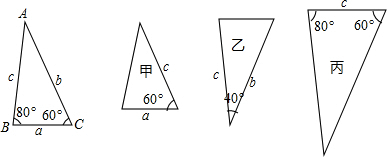
解答:在△ABC中,∠A=40°.
甲:只有一个对应边与一个对应角相等,故甲不符合条件;
乙:由两个对应边与这两个边的夹角相等,符合两个三角形全等的定理SAS;
丙:两个角对应相等,但是这两个角间的线段不相等,故丙不符合条件.
故选B.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目