题目内容
在一次燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度分别为y1(cm),y2(cm).已知y1(cm)与燃烧时间x(h)之间的关系如图所示;乙蜡烛燃烧前的高度为30 cm,燃烧时每小时缩短15 cm,完成下列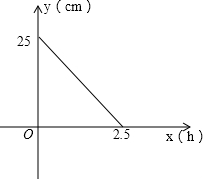 各题:
各题:
(1)甲蜡烛燃烧前的高度为______cm.燃烧时每小时缩短______cm.
(2)y2与x之间的函数关系式为______.
(3)在图中画出y2与x之间的函数图象;
(4)当y1<y2时,x的取值范围是______.
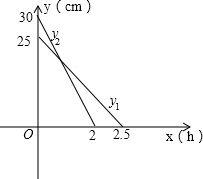 解:如图,
解:如图,(1)由上图可知甲蜡烛燃烧前的高度为25cm,燃烧时每小时缩短10cm;
(2)设出y2与x之间的一般函数关系式为y2=kx+b,把(0,30),(2,0)代入解得:
k=-15,b=30,所以y2=-15x+30;
(3)见上图;
(4)求得y1与y2的交点坐标为(1,15),由图象可以看出当时,x的取值范围是x<1.
分析:(1)由图形可以看出甲蜡烛燃烧前的高度和燃烧时每小时缩短的长度;
(2)设出y2与x之间的一般函数关系式y2=kx+b,代入(0,30),(2,0)两点即可求出;
(3)连接(0,30),(2,0)两点解决问题;
(4)先求出y1,y2的交点坐标,观察图形可得答案.
点评:此题考查用待定系数法一次函数解析式,数形结合,解决问题.

练习册系列答案
相关题目
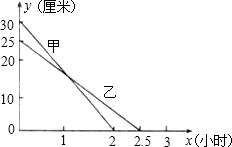 )与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: 22、在一次燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度分别为y1(cm),y2(cm).已知y1(cm)与燃烧时间x(h)之间的关系如图所示;乙蜡烛燃烧前的高度为30 cm,燃烧时每小时缩短15 cm,完成下列各题:
22、在一次燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度分别为y1(cm),y2(cm).已知y1(cm)与燃烧时间x(h)之间的关系如图所示;乙蜡烛燃烧前的高度为30 cm,燃烧时每小时缩短15 cm,完成下列各题: