题目内容
(本小题满分1 0分)
如图，已知线段AB∥CD，AD与B C相交于点K，E是线段AD上一动点。
【小题1】(1)若BK=
KC，求
的值；
【小题2】(2)连接BE，若BE平分∠ABC，则当AE= 
AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=
AD (n>2)，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．
【小题1】（1）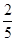
【小题2】（2）①猜想：AB=BC+CD，
证明：延长BE、DC交于点M
∵CD∥AB，AE=ED
∴△AEB≌△DEM
∴AB=MD=CD+MC，∠ABE=∠M
∵∠ABE=∠EBK
∴∠EBK=∠M
∴MC=BC
∴AB=BC+CD
②当AE=AD (n>2)，线段AB、BC、CD三者之间有如下等量关系：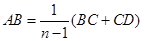
（
）
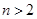解析
练习册系列答案
相关题目
（本小题满分6分，请在下列两个小题中，任选其一完成即可）
，并
来.
