题目内容
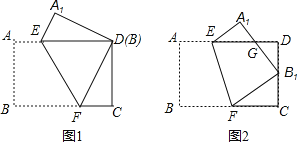
【题目】如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥l于E,过点C作CF⊥l于F,则下列说法中正确的是( )

A.AC=AE+BEB.EF=AE+EBC.AC=EB+CFD.EF=EB+CF
【答案】B
【解析】
证明△AEB≌△BFC,可得AE=BF,EB=CF,则结论得证.
解:∵AE⊥l,CF⊥l,
∴∠AEB=∠CFB=90°.
∴∠EAB+∠EBA=90°.
又∵∠ABC=90°,
∴∠EBA+∠CBF=90°.
∴∠EAB=∠CBF.
在△AEB和△BFC中
∵∠AEB=∠CFB,∠EAB=∠CBF,AB=BC,
∴△AEB≌△BFC(AAS).
∴AE=BF,EB=CF.
∴AE+CF=EB+BF.
即EF=AE+EB.
故选:B.

练习册系列答案
相关题目