Question

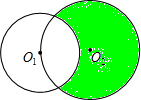如图，一个半径为3的圆O₁的圆心经过一个半径为3

2

的圆O₂，则图中阴影部分的面积为（　　）

• A、

  9

  2

• B、9
• C、9π-

  9

  2

• D、

  9π

  2

  -9

Answer 1

分析：连接O₁O₂，O₁A，O₁B，O₂A，O₂B，由勾股定理的逆定理得∠O₂CA=∠AO₂B=90°，则点A、O₁、B在同一条直线上，则AB是圆O₁的直径，从而得出阴影部分的面积S_阴影=

1

2

S_⊙1-S_弓形AO1B=

1

2

S_⊙1-（S_扇形AO2B-S_△AO2B）．

解答：解：连接O₁O₂，O₁A，O₁B，O₂A，O₂B，

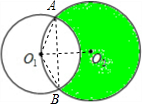
∵CO₂=CA=3，O₂A=3

2

，
∴CO₂²+CA²=O₂A²，
∴∠O₂CA=90°，同理∠O₂CB=90°，
∴点A、C、B在同一条直线上，并且∠AO₂B=90°，
∴AB是圆O₁的直径，
∴S_阴影=

1

2

S_⊙1-S_弓形AO1B
=

1

2

S_⊙1-（S_扇形AO2B-S_△AO2B）
=

1

2

π•32-

1

4

π•(3

2

)2+

1

2

×3

2

×3

2

=9．
故选B．

点评：本题考查了扇形面积的计算、勾股定理和相交两圆的性质．